Systems of Linear Equations

A system of equations is a collection of 2 or more equations each containing 1 or more
variables. A system of linear equations has equations of the form a₁x₁+a₂x₂+· · ·+a_nx_n = b.

• A solution consists of values for the variables that satisfy (are solutions of) each
equation in the system. Solving the system of equations requires finding the solution
set, which is the set of all such solutions.

• A system of equations is called consistent if it has one or more solutions; otherwise
it is called inconsistent.

• A system of equations is called independent if it has exactly one solution and dependent
if it has more than one solution.

* System of Two Linear Equations in Two Variables

ax + by = h
cx + dy = k

with variables x and y, coefficients a, b, c and d, and constants h and k.

*Graphing Method

The graph of each equation is a line. There are three possible scenarios for
the solution set.

1. One Solution - lines intersect at a point (consistent, independent)
2. No Solutions - lines are parallel (inconsistent)
3. Infinitely Many Solutions - lines coincide (consistent, dependent)

*Substitution Method

Pick one equation and solve for one variable in terms of the other. Substitute
result into the other equation and solve resulting linear equation in one variable.
Substitute result back into result from first step and solve for the second
variable.

*Elimination Method

Elimination by addition involves the replacement of systems of equations with
simpler equivalent systems, by performing appropriate operations, until obtaining
a system with an obvious solution. This method is very important
because it is readily generalized to higher-order systems.

Operations that transform a system of equations into an equivalent system
include:

1. Interchanging two equations
2. Multiplying an equation by a nonzero constant
3. Adding a constant multiple of one equation to another

*Matrices

The system of equations

ax + by = h
cx + dy = k

can be represented without writing the symbols for the variables as an augmented
matrix.

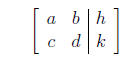
A matrix is a rectangular array of numbers written within brackets. Each
number in a matrix is called an element. If a matrix has m rows and n
columns, it is called an m × n matrix. The element in the ith row and jth
column of matrix A is denoted a_ij.

Operations that transform an augmented matrix into a row-equivalent matrix
include:

1. Interchanging two rows (R_i <--> R_j)
2. Multiplying a row by a nonzero constant (kR_i --> R_i)
3. Adding a constant multiple of one row to another (kR_j + R_i --> R_i)

Note: The arrow means “replace”.

Solving System: The system of equations represented by an augmented
matrix can be solved by transforming it into one of the following forms where
where m, n, and p are real numbers.

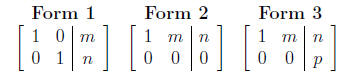
Form 1 - The system has an obvious unique solution.
Form 2 - The system has infinitely many solutions.
Form 3 - The system has no solution.

*Solving Linear Systems of Any Size

Any system of linear equations must have exactly one solution, no solution, or
infinitely many solutions.

*Gauss-Jordan Elimination

1. Choose the leftmost nonzero column and use appropriate row operations
to get a 1 at the top.
2. Use multiples of the row containing the 1 from step 1 to get zeros in all
remaining places in the column containing this 1.
3. Repeat step 1 using the submatrix formed using only rows below the row
used in step 2.
4. Repeat step 2 with the entire matrix and continue until it is impossible
to go further.

If at any point, a row is obtained with all zeros to the left of the vertical line,
and a nonzero to the right, stop because there is no solution.

If the number of leftmost 1’s in the resulting matrix is less than the number of
variables in the system and there are no contradictions, then the system has
infinitely many solutions.

*Systems of Linear Inequalities in Two Variables

*Graphing
• a vertical line divides a plane into left and right half-planes

• a non-vertical line divides a plane into upper and lower half-planes

• For an inequality Ax + By < C, Ax + By ≤C, Ax + By > C, or
Ax + By ≥C with B ≠ 0, the graph is either the lower or upper halfplane
(but not both) determined by the line Ax + By = C.

Steps to Graph Inequality in Two Variables
1. Graph the line Ax + By = C as a dashed line if equality is not
included in the original statement (< or >), or as a solid line if
equality is included ( ≤or≥ ).
2. Choose a test point anywhere in the plane not on the line and
substitute the coordinates into the inequality. (Hint: A common
test point is (0,0) because it is easy to evaluate.)
3. If the inequality is satisfied by the point, the graph is the half-plane
that includes the test point, otherwise, the graph is the half-plane
that does not include the test point.

• For the inequality Ax < C or Ax > C, the graph is either the left or
right half-plane (but not both) determined by the line Ax = C.

*Solving
• Graphical solution is to find the intersection of the graphs of all equations
in the system, called the solution region or feasible region.
• A corner point of a solution region is the intersection of two boundary
lines.
• The inequalities x ≥0 and y ≥0, called nonnegative restrictions, occur
frequently in applications involving systems in which x and y cannot
be negative.
• A solution region is bounded if it can be enclosed with a circle.
• A solution region is unbounded if it cannot be enclosed with a circle.

 *Linear Programming