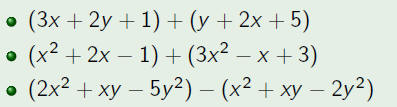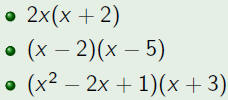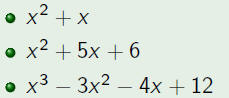Algebraic Thinking

Outline

1 What is Algebra?
2 Algebra and Graphs
3 Algebraic Manipulations
4 Conclusion

Examples of Algebra

Many people find the thought of algebra, equations, and variables
intimidating. But it is just generalized arithmetic.

Algebraic Examples

Consider the following common uses of algebra.

•Formulas – (C = πd)
Relation between two or more variables
•Equations – (5x = 30)
Finding an unknown value
•Identities – (sin²x + cos²x = 1)
An expression true for any x
•Property – (a + b = b + a)
Expression of a general rule
•Function – (f (x) = 3x + 1)
An input (independent) and output (dependent) variable

Examples of Using Algebra

Let’s look at a few examples from this list.

Formulas

The formula 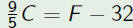  relates temperatures in Farenheit to temperatures in Celsius. Use this formula to convert 20 degrees cesius to farenheit and 41 degrees farenheit to celsius.

Equations

Fill in the blank.

Properties

Use symbols to express the fact that every number has an additive inverse.

Algebra as a Study of Structure

There are many different ways to view algebra.

Study of Structure

Algebra can be seen as a study of structure. That is, what is the structure of arithmetic? How does it work?

Example

For all real numbers a, b and c the following laws hold: a + b = b + a commutative law of addition (a + b) + c = a + (b + c) associative law of addition a + (−a) = 0 additive inverses a + 0 = a additive identity

Algebra as a Study of Relationships

Another way to view algebra is a method to express relationships.

Relationships Between Quantities

Algebra can be seen as a study of the relationship between quantities. The concept of a function is important here as there is usually an “input” quantity and an “output” quantity.

Example

A phone card has a connection fee of $0.25 plus a $0.05/minute charge for the actual time of the call. Describe the price of the call as a function of the number of minutes spent on the call.

Use the following methods to express the relationship above

•a table •a graph •a function rule

Using Graphs to Visualize Algebraic Relationships

As we saw in the previous example, graphs can be an important
way to visualize a relationship between quantities which can be
expressed algebraically.

Example

A beautician charges $15 for haircuts. Each week she has fixed expenses of $150. Express her profit as a function of teh number of haircuts she gives. Use a graph to describe this function.

Question

Are the table, graph, and formula we used to answer the previous question really accurate? In particular, is it possible to give 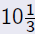haircuts? How is this problem seen in the graph?

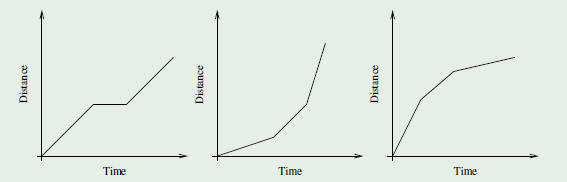
Interpreting Graphs

Many times a graph is enough to describe a relationship.

Example

Below are descriptions of three runners in a race. Match each description to the correct graph and explain your choice. •Alex started slowly, then ran a bit faster, and then ran even faster at the end of the race. •Manuel started quickly but then tired and slowed down a bit and then slowed down even more at the end. •Sara started quickly, stoped to tie her shoe, and then ran even faster than before.

Recalling Algebraic Rules

There are several symbolic rules to working with algebra which you
have learned in the past. Let’s review some of these rules.

Adding Polynomials

When adding polynomials group like terms together and use the distributive property (a(b + c) = ab + ac) to combine like terms.

Example

Add the following polynomials.

Multiplication and Factoring

Finally, we will briefly review multiplying and factoring.

Example

Multiply the following polynomials.

Example

Factor the following polynomials completely.

Important Concepts

Things to Remember from Section 2.2

1 Various uses of algebra 2 Solving equations 3 Representing relationships using fuctions and graphs 4 Adding, multiplying, and factorying polynomials