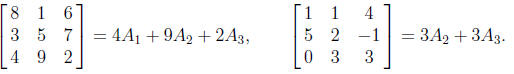- Home
- INTERMEDIATE ALGEBRA
- Course Syllabus for Algebra I
- Mid-Plains Community College
- FRACTION OF A WHOLE NUMBER
- Systems of Linear Equations
- MATH FIELD DAY
- Course Outline for Finite Mathematics
- Calculus
- Algebra Final Examination
- Math 310 Exam #2
- Review of Trigonometric Functions
- Math 118 Practice test
- Precalculus Review
- Section 12
- Literal Equations
- Calculus Term Definitions
- Math 327A Exercise 2
- Public Key Algorithms II
- Maximizing Triangle Area
- Precalculus I Review for Midterm
- REVIEW OF A FIRST COURSE IN LINEAR ALGEBRA
- Math 6310 Homework 5
- Some Proofs of the Existence of Irrational Numbers
- ALGEBRAIC PROPERTIES OF MATRIX OPERATIONS
- Math 142 - Chapter 2 Lecture Notes
- Math 112 syllabus
- Math 371 Problem Set
- Complex Numbers,Complex Functions and Contour Integrals
- APPLICATIONS OF LINEAR EQUATIONS
- Week 4 Math
- Fractions
- Investigating Liner Equations Using Graphing Calculator
- MATH 23 FINAL EXAM REVIEW
- Algebra 1
- PYTHAGOREAN THEOREM AND DISTANCE FORMULA
- Georgia Performance Standards Framework for Mathematics - Grade 6
- Intermediate Algebra
- Introduction to Fractions
- FACTORINGS OF QUADRATIC FUNCTIONS
- Elementary Algebra Syllabus
- Description of Mathematics
- Integration Review Solutions
- College Algebra - Applications
- A Tip Sheet on GREATEST COMMON FACTOR
- Syllabus for Elementary Algebra
- College Algebra II and Analytic Geometry
- Functions
- BASIC MATHEMATICS
- Quadratic Equations
- Language Arts, Math, Science, Social Studies, Char
- Fractions and Decimals
- ON SOLUTIONS OF LINEAR EQUATIONS
- Math 35 Practice Final
- Solving Equations
- Introduction to Symbolic Computation
- Course Syllabus for Math 935
- Fractions
- Fabulous Fractions
- Archimedean Property and Distribution of Q in R
- Algebra for Calculus
- Math112 Practice Test #2
- College Algebra and Trigonometry
- ALGEBRA 1A TASKS
- Description of Mathematics
- Simplifying Expressions
- Imaginary and Complex Numbers
- Building and Teaching a Math Enhancement
- Math Problems
- Algebra of Matrices Systems of Linear Equations
- Survey of Algebra
- Approximation of irrational numbers
- More about Quadratic Functions
- Long Division
- Algebraic Properties of Matrix Operation
- MATH 101 Intermediate Algebra
- Rational Number Project
- Departmental Syllabus for Finite Mathematics
- WRITTEN HOMEWORK ASSIGNMENT
- Description of Mathematics
- Rationalize Denominators
- Math Proficiency Placement Exam
- linear Equations
- Description of Mathematics & Statistics
- Systems of Linear Equations
- Algebraic Thinking
- Study Sheets - Decimals
- An Overview of Babylonian Mathematics
- Mathematics 115 - College Algebra
- Complex Numbers,Complex Functions and Contour Integrals
- Growing Circles
- Algebra II Course Curriculum
- The Natural Logarithmic Function: Integration
- Rational Expressions
- QUANTITATIVE METHODS
- Basic Facts about Rational Funct
- Statistics
- MAT 1033 FINAL WORKSHOP REVIEW
- Measurements Significant figures
- Pre-Calculus 1
- Compositions and Inverses of Functions
Systems of Linear Equations
1. True or False.
(a) The null space of a 4 × 6 real matrix is a subspace of R6.
(b) The column space of a 4 × 6 real matrix is a subspace of R6.
(c) The rank of a 6 × 4 real matrix is at most 4.
(d) The nullity of a 4 × 6 real matrix is at least 4.
(e) A vector 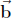 in Rm is in the column space of an m × n real matrix A if the
linear
in Rm is in the column space of an m × n real matrix A if the
linear
system 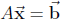 is solvable.
is solvable.
(f) Any vector in the range of an m × n real matrix A can be written as a linear
combination of the column vectors of A.
(g) Suppose that an m × n real matrix A is row reduced to another matrix B by row
reductions. Then the null space of A equals the null space of B.
(h) Suppose that an m × n real matrix A is row reduced to another matrix B by row
reductions. Then the range of A equals the range of B.
(i) Suppose that an m × n real matrix A is row reduced to another matrix B by row
reductions. Then rank(A) = rank(B) and nullity(A) = nullity(B).
(j) If the column vectors of a 6 × 4 real matrix A are linearly independent, then
the null
space of A is { 0 }.
(k) If the column vectors of a 6 × 4 real matrix A are linearly independent, then
the
column space of A is R6.
2. Let 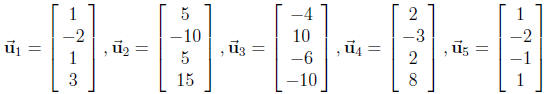 .
.
(a) Find the dimension and a basis of Span
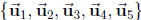 .
.
(b) Find the dimension and a basis of Span 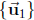 . Is
. Is
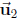 in Span
in Span 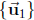 ? If yes,
write it as
? If yes,
write it as
a scalar multiple of 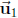 with a specific
coefficient.
with a specific
coefficient.
(c) Find the dimension and a basis of Span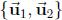 . Is
. Is
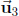 in Span
in Span 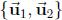 ?
If yes, write
?
If yes, write
it as a linear combination of 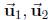 with specific
coefficients.
with specific
coefficients.
(d) Find the dimension and a basis of Span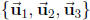 . Is
. Is
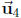 in Span
in Span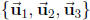 ? If
? If
yes, write it as a linear combination of 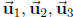 with specific
coefficients.
with specific
coefficients.
(e) Find the dimension and a basis of Span 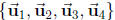 Is
Is
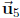 in
Span
in
Span 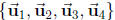 ?
?
If yes, write it as a linear combination of 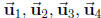 with specific
coefficients.
with specific
coefficients.
Hint: The row reduction of one single matrix provides the answers to all these
questions.
3. A n × n square matrix is called a magic square if its n
row sums, n column sums, and 2
diagonal sums are all equal. For instance,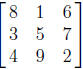 is
a 3 × 3 magic square, since
is
a 3 × 3 magic square, since
8+1+6 = 3+5+7 = 4+9+2 = 8+3+4 = 1+5+9 = 6+7+2 = 8+5+2 = 6+5+4:
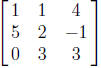 is another one.
is another one.
Let V be the vector space of all 3 × 3 real matrices, and let M be the set of all
3 × 3
magic squares with real entries.
(a) Show that M is a subspace of V .
(b) Find the dimension and a basis of M.
Answers:
1. (a) Y (b) N (c) Y (d) N (e) Y (f) Y (g) Y (h) N (i) Y (j) Y (k) N
2. (a) dim = 3. Basis: 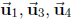 .
.
(b) dim = 1. Basis: ![]() . Yes,
. Yes,
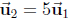 .
.
(c) dim = 1. Basis: ![]() . No.
. No.
(d) dim = 2. Basis: 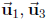 . No.
. No.
(e) dim = 3. Basis: 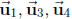 . Yes,
. Yes,
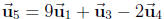 .
.
3. (a) Verify by yourself. I'll skip here.
(b) dim(M) = 3. The following matrices form a basis of M:
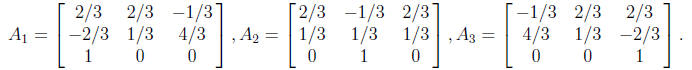
Remark 1: Of course you may have different choices. That's
just fine, as long as your
basis consists of 3 different magic squares and they span M.
Remark 2: Solving this problem allows us to generate all 3 × 3 magic squares. For
the
example matrices given in the problem we have the following: